无限图着色问题的关键数值差异集中在二色与三色方案之间：二色会导致不可测的散点集，而三色能生成可测的弧段，从而将问题从层级最低档提升到可度量的高阶层。此差异对应集合长度可计算与不可计算的根本分界，构成描述集合论问题分类的主要比值门槛。Bernshteyn 识别到这一结构在多类着色问题中重复出现，指向一个统一机制。

在计算机科学中，本地算法对有限图要求以固定步数收敛，而二色本地算法在路由器干扰模型中必然极度低效，对比三色算法可在显著更少轮次内完成任务；因此颜色数量与所需轮次呈高度非线性关系。讲座中呈现的阈值结构与描述集合论中的可测着色阈值高度同构，二色对应效率崩溃，三色对应可行区域，形成跨领域的颜色–复杂度临界线。

Bernshteyn 的目标是证明：每个高效本地算法都能转换为满足勒贝格可测性的无限图着色方案，使计算机科学中的效率层级与集合论中的可测性层级一一对应。其核心在于算法只需访问局部邻域并为局部节点赋唯一标签，此要求在有限图中可通过一对一编号完全满足，从而支撑将有限图局域性推广到具有可测结构的无限图。

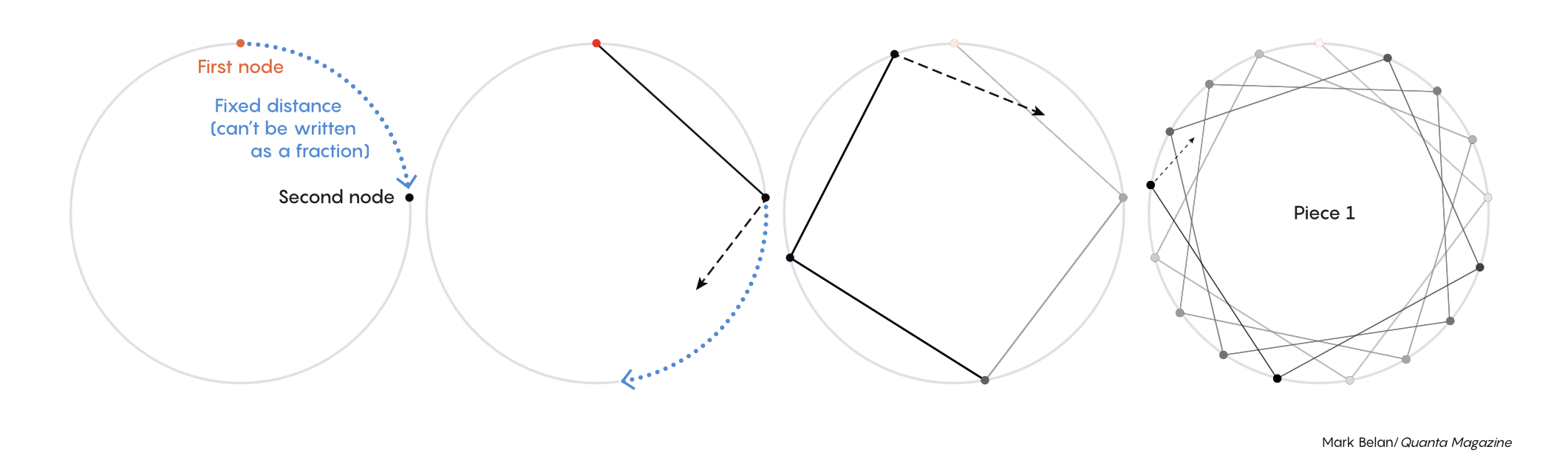
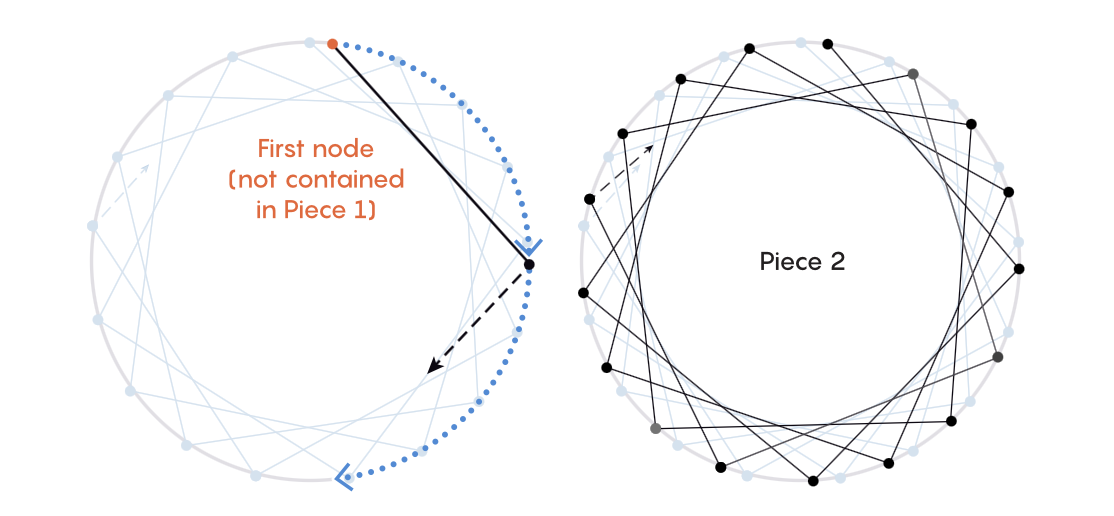
The key quantitative divide in infinite graph coloring lies between two-color and three-color schemes: two colors yield nonmeasurable scattered sets, while three colors produce measurable arcs, moving the task from the lowest tier to a higher measurable tier. This difference corresponds to a sharp boundary between computable and noncomputable lengths, forming the main ratio-based threshold used to classify problems in descriptive set theory. Bernshteyn identified a recurring structure suggesting a unifying mechanism.

In computer science, local algorithms on finite graphs must converge in bounded rounds, yet any two-color local algorithm in the router-interference model is necessarily highly inefficient, whereas a three-color algorithm completes in far fewer rounds; the number of colors thus correlates nonlinearly with round complexity. The thresholds presented in the talk mirrored those in descriptive set theory, with two colors marking failure and three colors opening the feasible region, creating a cross-disciplinary color–complexity boundary.

Bernshteyn aimed to show that every efficient local algorithm can be converted into a Lebesgue-measurable coloring of an infinite graph, aligning efficiency tiers in computer science with measurability tiers in set theory. The core lies in the algorithm’s reliance on local neighborhoods and unique labels, feasible in finite graphs via one-to-one numbering, enabling the extension of locality to measurable infinite structures.