这一研究解决了一个源自19世纪的拓扑学问题：不同形状是否可能由相同的局部几何数据所定义。研究团队在一个夏天里对“犀牛”这一离散曲面进行深入分析，常常在视频通话中连续工作8至12小时。关键线索来自沿曲面边缘闭合的曲率线，这些线条始终位于平面或球面上，而非随机分布于三维空间，这种高度受限的几何行为被认为几乎不可能是偶然出现的。

研究人员随后转向光滑曲面，试图寻找具有类似性质的连续对应物。尽管光滑曲面没有边，但仍可定义最大与最小弯曲方向的曲率线。一个多世纪前，法国数学家达布提出的公式恰好描述了这类曲面，但其曲率线会发散成螺旋并趋于无穷，无法闭合，因此不能形成环面。通过多年推导与计算实验，团队成功修改了这些公式，使曲率线能够闭合，从而首次构造出满足条件的光滑“犀牛”。

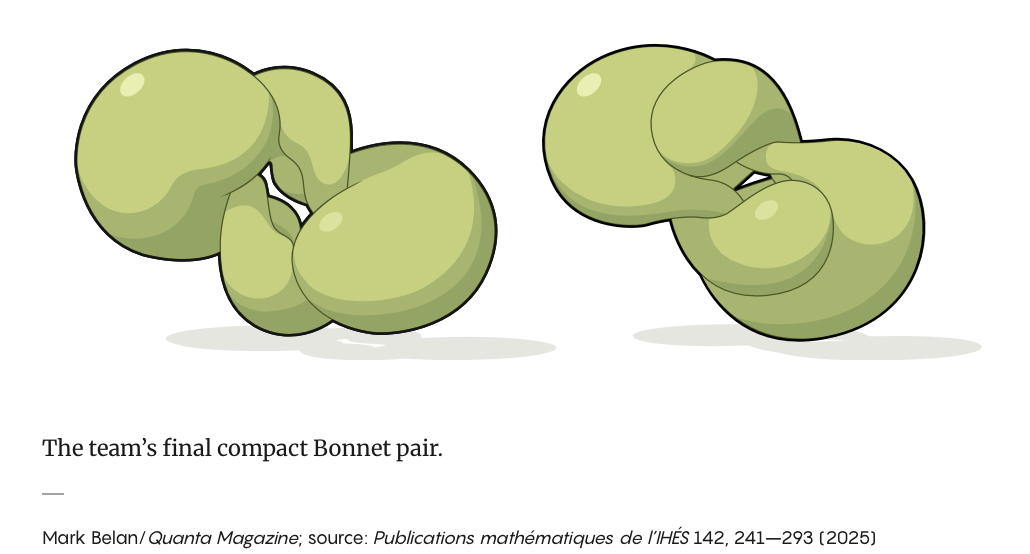
这一曲面最终生成了一对新的环面，它们具有相同的度量和平均曲率，却在整体结构上不同，从而给出了Bonnet问题的反例。最初得到的环面对只是彼此的镜像；在接下来一年中，研究人员进一步放宽约束，最终构造出一对明显不同、形态高度扭曲但仍共享相同局部数据的环面，完整解决了这一延续数百年的数学难题。

This work resolved a topology problem dating back to the 19th century: whether distinct shapes can be defined by identical local geometric data. Over a summer, the researchers intensively studied a discrete surface known as the “rhino,” often working in video calls for 8 to 12 hours at a time. A key clue came from closed curvature lines along the surface’s edges, which always lay in planes or on spheres rather than wandering freely through three-dimensional space, a constraint considered extremely unlikely to be coincidental.

The team then turned to smooth surfaces in search of a continuous analogue. Although smooth surfaces lack edges, they still admit curvature lines marking directions of maximum and minimum bending. More than a century ago, the French mathematician Jean Gaston Darboux had derived formulas describing such surfaces, but his curvature lines spiraled off to infinity and never closed, preventing the formation of a torus. After years of analytical work and computational experimentation, the researchers modified these formulas so the curvature lines would close, yielding the first suitable smooth “rhino.”

This surface produced a pair of tori sharing the same metric and mean curvature but differing globally, providing a counterexample to the Bonnet problem. The initial pair turned out to be mirror images, which was formally sufficient but unsatisfying. Over the next year, the team relaxed certain constraints and constructed a new version, ultimately generating a pair of highly twisted, visibly distinct tori that still shared identical local data, fully resolving the centuries-old puzzle.